Clinical research studies and healthcare economics studies are frequently concerned with assessing the prognosis for survival in circumstances where patients suffer from a disease that progresses from state to state. Standard survival models only directly model two states: alive and dead. Multi-state models enable directly modeling disease progression where patients are observed to be in various states of health or disease at random intervals, but for which, except for death, the times of entering or leaving states are unknown. Multi-state models easily accommodate interval censored intermediate states while making the usual assumption that death times are known but may be right censored.
A natural way to conceptualize modeling the dynamics of disease progression with interval censored states is as continuous time Markov chains. The following diagram illustrates a possible disease progression model where there is some possibility of dying from any state, but otherwise a patient would progress from being healthy, to mild disease, to severe disease and then perhaps death.
## Loading required package: shape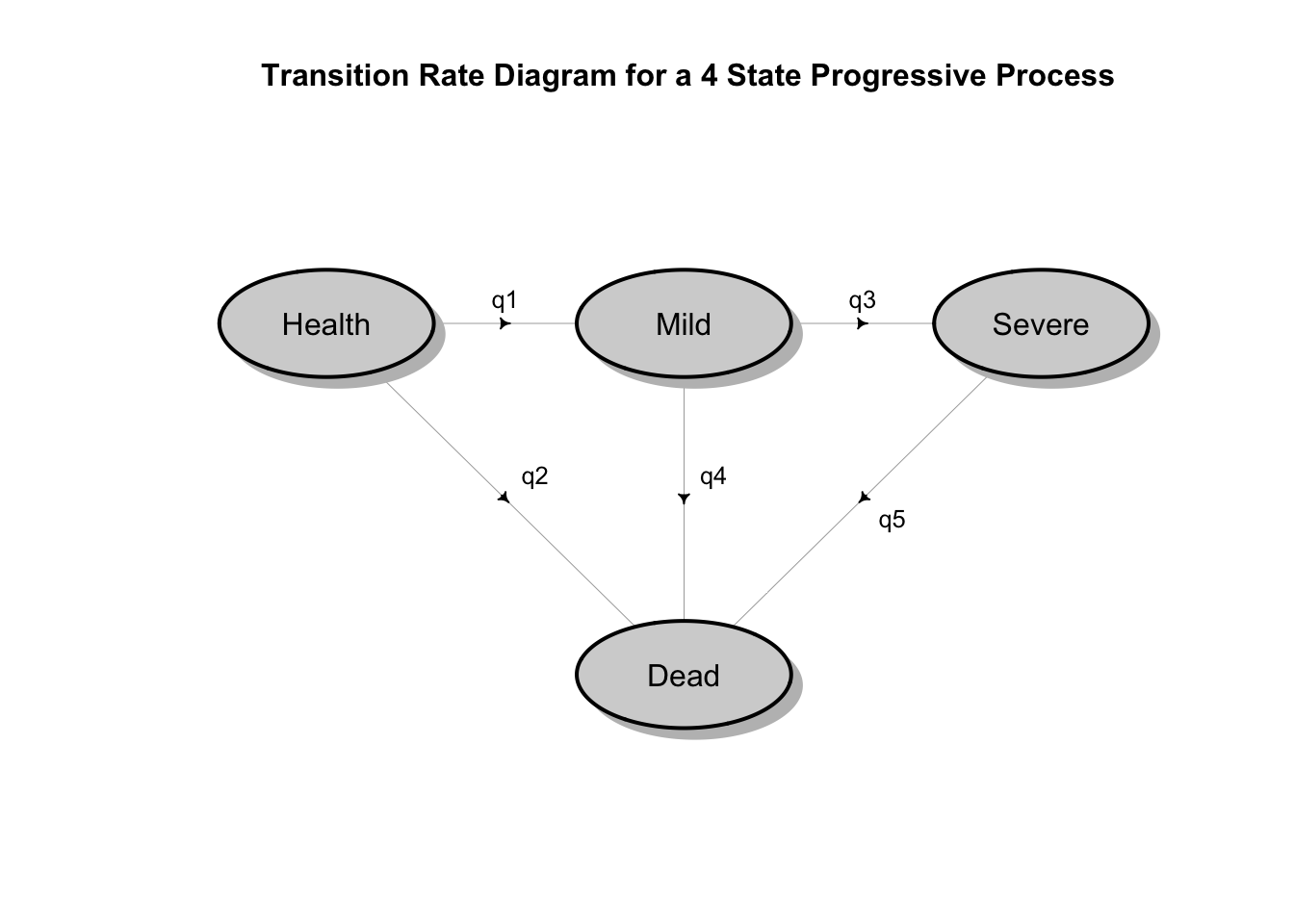 It is true that in that the Markov assumption implies that the time patients spend in the various states are exponentially distributed. However, the mathematical theory of stochastic multi-state processes is very rich and can accommodate more realistic models with state dependent hazard rates that vary over time and other relaxations of the Markov assumption. Moreover, there is robust software in R (and other languages) that make multi-state stochastic survival models practical.
It is true that in that the Markov assumption implies that the time patients spend in the various states are exponentially distributed. However, the mathematical theory of stochastic multi-state processes is very rich and can accommodate more realistic models with state dependent hazard rates that vary over time and other relaxations of the Markov assumption. Moreover, there is robust software in R (and other languages) that make multi-state stochastic survival models practical.
In the remainder of this post, I present a variation of a disease progression model discussed by Ardo van den Hout in some detail in his incredibly informative and very readable monograph Multi-State Survival Models for Interval Censored Data . Also note that van den Hout’s model is itself an elaboration of the main example presented by Christopher Jackson in the vignette to his msmpackage. This post presents a slower development of the model developed by Jackson and van den Hout that might be easier for a person not already familiar with the msm package to follow.
library(tidyverse)
library(tidymodels)
library(msm)The Data
The data set explored by both Jackson and van den Hout is the Cardiac Allograft Vasculopathy (CAV) data set which contains the individual histories of angiographic examinations of 622 heart transplant recipients collected at the Papworth Hospital in the United Kingdom. This data is included in the msm package and is a good candidate to be the iris dataset for progressive disease models. It is a rich data set with 2846 rows and multiple covariates, including patient age and time time since transplant, both of which can be use for time scales, multiple state transitions among four states and no missing values. Observations of intermediate states are interval censored and have been recorded varying time intervals. Deaths are “exact” or right censored.
The following code creates a new variable that preserves the original state data for each observation and displays the data in tibble format.
set.seed(1234)
df <- tibble(cav) %>% mutate(o_state = state)
df## # A tibble: 2,846 × 11
## PTNUM age years dage sex pdiag cumrej state firstobs statemax o_state
## <int> <dbl> <dbl> <int> <int> <fct> <int> <int> <int> <dbl> <int>
## 1 100002 52.5 0 21 0 IHD 0 1 1 1 1
## 2 100002 53.5 1.00 21 0 IHD 2 1 0 1 1
## 3 100002 54.5 2.00 21 0 IHD 2 2 0 2 2
## 4 100002 55.6 3.09 21 0 IHD 2 2 0 2 2
## 5 100002 56.5 4 21 0 IHD 3 2 0 2 2
## 6 100002 57.5 5.00 21 0 IHD 3 3 0 3 3
## 7 100002 58.4 5.85 21 0 IHD 3 4 0 4 4
## 8 100003 29.5 0 17 0 IHD 0 1 1 1 1
## 9 100003 30.7 1.19 17 0 IHD 1 1 0 1 1
## 10 100003 31.5 2.01 17 0 IHD 1 3 0 3 3
## # ℹ 2,836 more rowsThe state table which presents the number of times each pair of states were observed in successive observation times shows that 46 transitions from state 2 (Mild CAV) to state 1 (No CAV), 4 transitions from state 3 (Severe CAV) to Healthy and 13 transitions from Severe CAV to Mild CAV.
statetable.msm(state = state, subject = PTNUM, data = df)## to
## from 1 2 3 4
## 1 1367 204 44 148
## 2 46 134 54 48
## 3 4 13 107 55I will follow van den Hout and assume these backward transitions are misclassified and alter the state variable so there is no back sliding. The following code does this in a tidy way and also creates a new variable b_age which records the baseline age at which patients entered the study. (Note: you can find van den Hout’s code here)
df1 <- df %>% group_by(PTNUM) %>%
mutate(b_age = min(age),
state = cummax(state)
)This transformation will make the state transition table conform to the diagram above, but with state 1 representing No CAV rather than Health.
statetable.msm(state = state, subject = PTNUM, data = df1)## to
## from 1 2 3 4
## 1 1336 185 40 139
## 2 0 220 52 49
## 3 0 0 140 63Setting Up and Running the Model
The next step is to set up the model using the function msm() whose great flexibility means that some care must be taken to set parameter values.
First, we set up the initial guess for the intensity matrix, Q, which determines the transition rates among states for a continuous time Markov chain. For the msm function, positive values indicate possible transitions.
# Intensity matrix Q:
q <- 0.01
Q <- rbind(c(0,q,0,q), c(0,0,q,q),c(0,0,0,q),c(0,0,0,0))
qnames <- c("q12","q14","q23","q24","q34")Next, we set up the covariate structure which van den Hout discusses in his monograph, but does not show in the code on the book’s website referenced above. For this model, transitions from state 1 to state 2 and from state 1 to state 4 depend on time,years, the age of the patient at transplant time b_age, and dage, the age of the donor. The other transitions depend only on dage. So, we see that msm() can deal with time varying covariates as well as permitting individual state transitions to be driven by different covariates.
covariates = list("1-2" = ~ years + b_age + dage ,
"1-4" = ~ years + b_age + dage ,
"2-3" = ~ dage,
"2-4" = ~ dage,
"3-4" = ~ dage)Now, we set the remaining parameters for the model.
obstype <- 1
center <- FALSE
deathexact <- TRUE
method <- "BFGS"
control <- list(trace = 0, REPORT = 1)obstype = 1 indicates that observations have been taken at arbitrary time points. They are snapshots of the process that are common for panel data.
center = FALSE means that covariates will not be centered at their means during the maximum likelihood estimation process. The default for this parameter is TRUE.
deathexact = TRUE indicates that the final absorbing state is exactly observed. This is the defining assumption survival data. In msm this is equivalent to setting obstupe = 3 for state 4, our absorbing state.
** method = BFGS** signals optim() to use the optimization method published simultaneously in 1970 by Broyden, Fletcher, Goldfarb and Shanno. (look here). This is a quasi-Newton method that uses function values and gradients to build up a picture of the surface to be optimized.
control = list(trace=0,REPORT=1) indicates more parameters that will be passed to optim().
REPORT sets the the frequency of reports for the “BFGS”, “L-BFGS-B” and “SANN” methods if control$trace is positive. Defaults to every 10 iterations for “BFGS” and “L-BFGS-B”, or every 100 temperatures for “SANN”. (Note: SANN is a variant of the simulated annealing method presented by C. J. P. Belisle (1992) Convergence theorems for a class of simulated annealing algorithms on Rd Journal of Applied Probability.)
trace is also passed tooptim(). trace must be a non-negative integer. If positive, tracing information on the progress of the optimization is produced. Higher values may produce more tracing information.
model_1 <- msm(state~years, subject = PTNUM, data = df1, center= center,
qmatrix=Q, obstype = obstype, deathexact = deathexact, method = method,
covariates = covariates, control = control)First check to see if the model has converged. For the BFGS method, possible convergence codes returned by optim() are:
0 indicates convergence, 1 indicates that the maximum iteration limit has been reached, 51 and 52 indicate warnings.
#Model Status
conv <- model_1$opt$convergence; cat("Convergence code =", conv,"\n")## Convergence code = 0Next, look at a measure of how well the model fits the data proposed by using a visual test proposed by Gentleman et al. (1994) which plots the observed numbers of individuals occupying a state at a series of times against forecasts from the fitted model, for each state. The msm function plot.prevalence.msm() produces a perfectly adequate base R plot. However, to emphasize that msm users are not limited to base R plots, I’ll do a little extra work to use ggplot(). When a package author is kind enough to provide an extractor function you can do anything you want with the data.
The prevalence.msm() function extracts both the observed and forecast prevalence matrices.
prev <- prevalence.msm(model_1)This not very elegant, but straightforward code reshapes the data and plots.
# reshape observed prevalence
do1 <-as_tibble(row.names(prev$Observed)) %>% rename(time = value) %>%
mutate(time = as.numeric(time))
do2 <-as_tibble(prev$Observed) %>% mutate(type = "observed")
do <- cbind(do1,do2) %>% select(-Total)
do_l <- do %>% gather(state, number, -time, -type)
# reshape expected prevalence
de1 <-as_tibble(row.names(prev$Expected)) %>% rename(time = value) %>%
mutate(time = as.numeric(time))
de2 <-as_tibble(prev$Expected) %>% mutate(type = "expected")
de <- cbind(de1,de2) %>% select(-Total)
de_l <- de %>% gather(state, number, -time, -type)
# bind into a single data frame
prev_l <-rbind(do_l,de_l) %>% mutate(type = factor(type),
state = factor(state),
time = round(time,3))
# plot for comparison
prev_gp <- prev_l %>% group_by(state)
pp <- prev_l %>% ggplot() +
geom_line(aes(time, number, color = type)) +
xlab("time") +
ylab("") +
ggtitle("")
pp + facet_wrap(~state)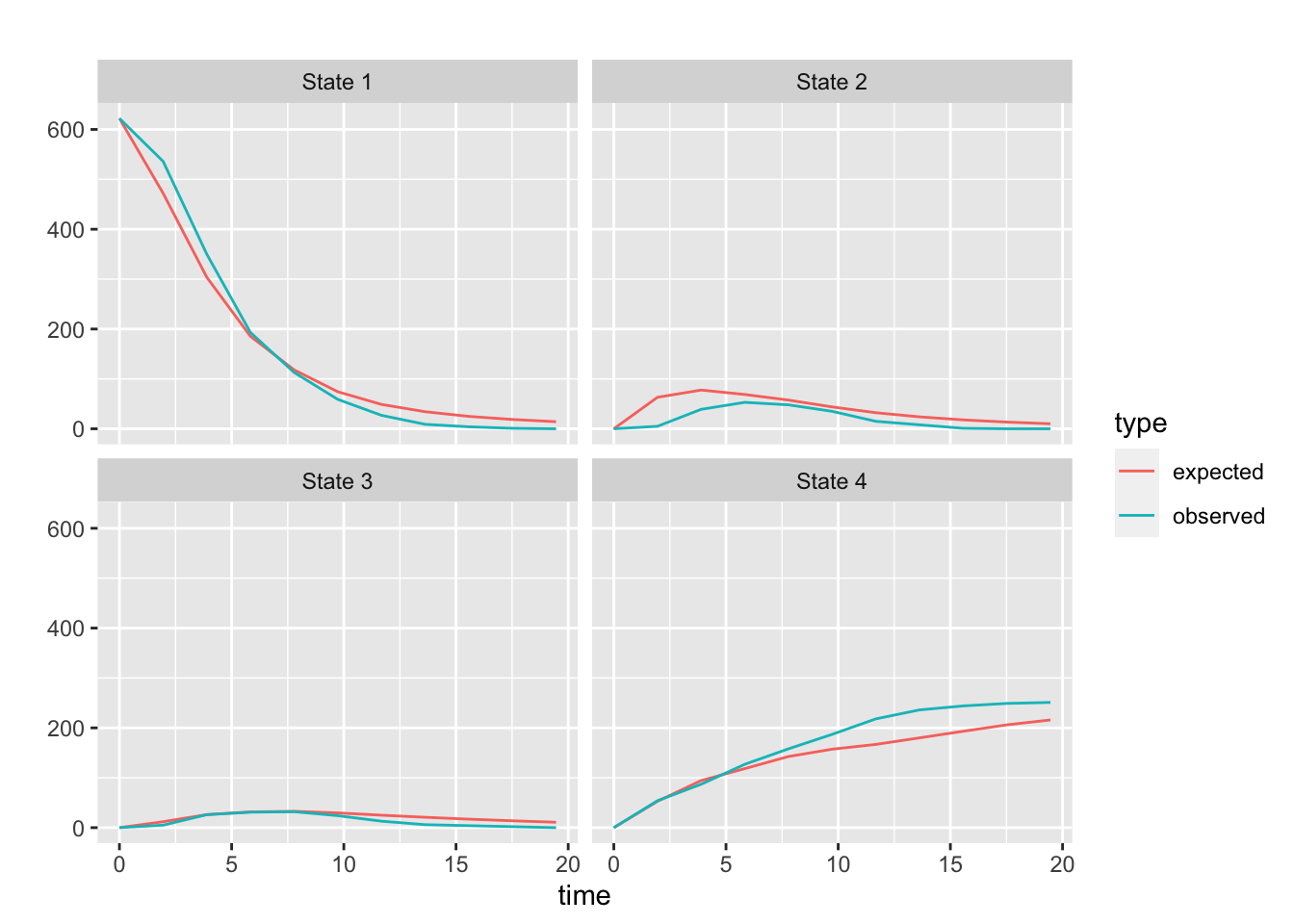
The agreement of the observed and forecast prevalence for states 1 through 3 look pretty good. After about 8 years the observed deaths are notably higher than the forecast. As Jackson points out (See the msm Manual page 33), this kind of discrepancy could indicate that the underlying process is not homogeneous. I have attempted to capture this non-homogeneity by having some of the transitions depend on time. And, although the plot above looks a little better that than the plot in the manual, which does not attempt to model non-homogeneity, it is apparent that there is room to find a better model!
Survival Curves and Calculations
Now, we can jump straight to the major result and look at the fitted survival curves. There is a plot() method for msm that will directly plot these curves. However, just to emphasize that if a package author is kind enough to provide a plot method, it will probably not be too difficult to hack the code for the method to use an alternative plotting system. To save space, I will not show my code, but you can easily recreate it by stating with the plot.msm() function, deleting the plotting parts and returning the values for time and the states “Health, Mild_CAV, and Severe_CAV which are used int the code below. Check my hack by running plot(model_1)
# plot_prep was obtained from plot.msm()
res <- plot_prep(model_1)
time <- res[[1]]
Health <- res[[2]]
Mild_CAV <- res[[3]]
Severe_CAV <- res[[4]]
df_w <- tibble(time,Health, Mild_CAV, Severe_CAV)
df_l <- df_w %>% gather("state", "survival", -time)
p <- df_l %>% ggplot(aes(time, 1 - survival, group = state)) +
geom_line(aes(color = state)) +
xlab("Years") +
ylab("Probability") +
ggtitle("Fitted Survival Probabilities")
p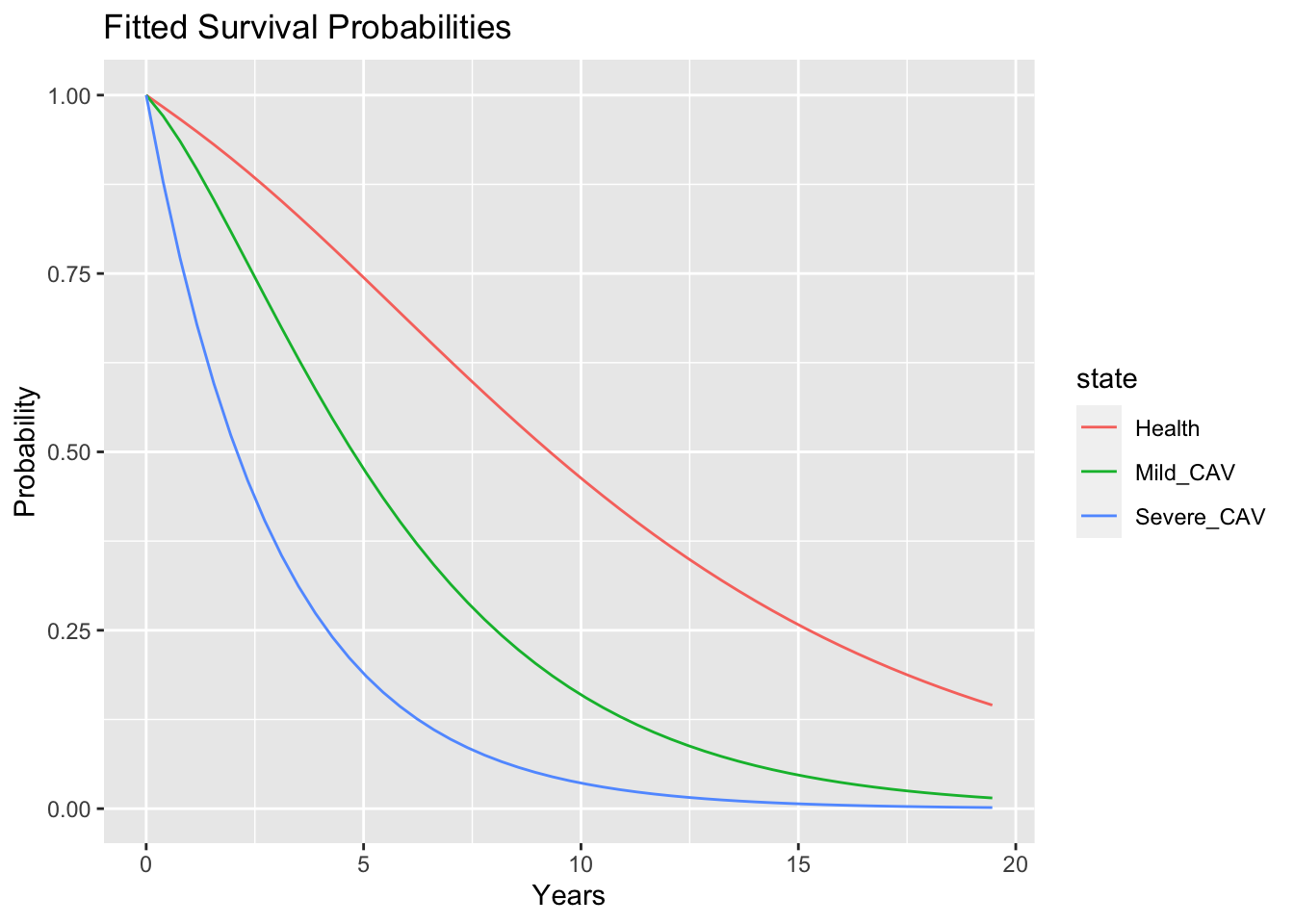
These curves indicate that a treatment that could prevent CAV or at least delay progression from mild CAV to severe CAV might prolong survival. Additionally, the Markov structure of the model permits extracting information that relates to disease progression and the total time spent in each state.
The function totlos.msm() estimates the total expected time that a patient will spend in each state. Parameter settings for this function include:
start = c(1,0,0,0) specifies that patients will start in state 1 with probability 0.
fromt = 0 indicates starting at the beginning of the process.
covariates = “mean” indicates that the covariates will be set to their mean values for the calculation.
total_state_time <-totlos.msm(model_1,start = c(1,0,0,0), from = 0, covariates = "mean")
total_state_time## State 1 State 2 State 3 State 4
## 7.002 2.473 1.621 InfThe table indicates that the mean time a patient can expect to avoid CAV is about 7 years. After progressing to a Mild_CAV, a patient can expect five additional years.
A more direct calculation based on the intensity matrix, Q, give the expected time to the “absorbing” state, Death, from each of the “transient” living states.
time_to_death <- efpt.msm(model_1, tostate = 4, covariates = "mean")
time_to_death## [1] 11.097 5.836 3.005 0.000This agrees with the total state times calculated above.
sum(total_state_time[1:3])## [1] 11.1Within the scope of the information provided by the covariates, it is also possible to generate more individualized forecasts. For example, here is the expected time to death for a person starting off with no CAV at age 60, who received a heart from a 20 year old donor, 5 years after the transplant.
efpt.msm(model_1, tostate = 4, start = c(1,0,0,0), covariates = list(years = 5, b_age = 60, dage = 20))## [,1]
## [1,] 7.953A related quantity, mean sojourn time, is the mean time that each visit to each state is expected to last. Since, we are assuming a progressive disease model where each patient visits each state only once, the estimate should be close to total time spent in each state. However, Jackson notes that in a progressive model, sojourn time in the disease state will be greater than the expected length of stay in the disease state because the mean sojourn time in a state is conditional on entering the state, whereas the expected total time in a diseased state is a forecast for an individual, who may die before getting the disease. (See help(totlos.msm)). And indeed, that is what we see here for states 2 and 3.
sojourn.msm(model_1, covariates="mean")## estimates SE L U
## State 1 7.002 0.4024 6.256 7.837
## State 2 3.525 0.3020 2.980 4.169
## State 3 3.005 0.3748 2.353 3.837Hazard Ratios
model_1 will also product estimates of hazard ratios which show the estimate effect on transition intensities for each state.
Here is the table of Hazard Ratios:
model_1##
## Call:
## msm(formula = state ~ years, subject = PTNUM, data = df1, qmatrix = Q, obstype = obstype, covariates = covariates, deathexact = deathexact, center = center, method = method, control = control)
##
## Maximum likelihood estimates
## Baselines are with covariates set to 0
##
## Transition intensities with hazard ratios for each covariate
## Baseline years
## State 1 - State 1 -0.032750 (-0.0607897,-0.017644)
## State 1 - State 2 0.030957 ( 0.0160470, 0.059721) 1.112 (1.061,1.166)
## State 1 - State 4 0.001793 ( 0.0004703, 0.006836) 1.093 (1.012,1.182)
## State 2 - State 2 -0.395633 (-0.6488723,-0.241227)
## State 2 - State 3 0.264310 ( 0.1488153, 0.469441) 1.000
## State 2 - State 4 0.131323 ( 0.0330133, 0.522385) 1.000
## State 3 - State 3 -0.434548 (-0.9113857,-0.207192)
## State 3 - State 4 0.434548 ( 0.2071918, 0.911386) 1.000
## b_age dage
## State 1 - State 1
## State 1 - State 2 1.001 (0.9884,1.014) 1.0281 (1.0159,1.040)
## State 1 - State 4 1.053 (1.0271,1.079) 1.0208 (1.0039,1.038)
## State 2 - State 2
## State 2 - State 3 1.000 0.9932 (0.9756,1.011)
## State 2 - State 4 1.000 0.9757 (0.9298,1.024)
## State 3 - State 3
## State 3 - State 4 1.000 0.9906 (0.9672,1.015)
##
## -2 * log-likelihood: 3466The table shows that time, the covariate years, affects disease progression represented by the the transition from state 1 to state 2, but has a smaller effect on the transition from state 1 to state 4.
The covariate b_age, the baseline age of patient at transplant time has a larger effect on dying before the onset of CAV than on the transition to CAV.
The covariate dage has a minor effect on the transitions from state 1 but apparently has no effect thereafter.
The hazard ratios are computed by calculating the exponential of the estimated covariate effects on the log-transition intensities for the Markov process which are stored in the model object.
To see how these work, first look at the baseline hazard ratios.
model_1$Qmatrices$baseline## State 1 State 2 State 3 State 4
## State 1 -0.03275 0.03096 0.0000 0.001793
## State 2 0.00000 -0.39563 0.2643 0.131323
## State 3 0.00000 0.00000 -0.4345 0.434548
## State 4 0.00000 0.00000 0.0000 0.000000These baseline hazard ratios are computed from the model intensity matrix, Q, assuming no covariates. They can also be directly extracted from the model by qmatrix.msm() extractor function with covariates set to zero.
qmatrix.msm(model_1, covariates = 0)## State 1 State 2
## State 1 -0.032750 (-0.0607897,-0.017644) 0.030957 ( 0.0160470, 0.059721)
## State 2 0 -0.395633 (-0.6488723,-0.241227)
## State 3 0 0
## State 4 0 0
## State 3 State 4
## State 1 0 0.001793 ( 0.0004703, 0.006836)
## State 2 0.264310 ( 0.1488153, 0.469441) 0.131323 ( 0.0330133, 0.522385)
## State 3 -0.434548 (-0.9113857,-0.207192) 0.434548 ( 0.2071918, 0.911386)
## State 4 0 0The 95% confidence limits are computed by assuming normality of the log-effect.
A more representative value for the intensity matrix for this model can be obtained by setting the covariates to their expected mean values.
qmatrix.msm(model_1, covariates = "mean")## State 1 State 2
## State 1 -0.14281 (-0.15984,-0.12760) 0.10019 ( 0.08742, 0.11482)
## State 2 0 -0.28369 (-0.33556,-0.23984)
## State 3 0 0
## State 4 0 0
## State 3 State 4
## State 1 0 0.04262 ( 0.03339, 0.05441)
## State 2 0.21821 ( 0.17636, 0.26999) 0.06548 ( 0.03872, 0.11075)
## State 3 -0.33281 (-0.42498,-0.26064) 0.33281 ( 0.26064, 0.42498)
## State 4 0 0Next, we may want to examine the contribution of the covariate covariates to the hazard ratios. To take a particular example, look at the dage to the hazard ratios
model_1$Qmatrices$dage## State 1 State 2 State 3 State 4
## State 1 0 0.02771 0.000000 0.020575
## State 2 0 0.00000 -0.006783 -0.024625
## State 3 0 0.00000 0.000000 -0.009439
## State 4 0 0.00000 0.000000 0.000000and focus on the contribution of dage to the intensity matrix for the transition from state 3 to state 4 which is given as -0.009439 in the table above. Taking the exponential of this value, yields the hazard ratio for the dage state 3 to 4 transition in the hazard ratio’s table we got by printing out model_1 above.
exp(-.009439)## [1] 0.9906The hazard ratio tables for the remaining covariates are given by:
model_1$Qmatrices$years## State 1 State 2 State 3 State 4
## State 1 0 0.1064 0 0.08933
## State 2 0 0.0000 0 0.00000
## State 3 0 0.0000 0 0.00000
## State 4 0 0.0000 0 0.00000and
model_1$Qmatrices$b_age## State 1 State 2 State 3 State 4
## State 1 0 0.0009645 0 0.05152
## State 2 0 0.0000000 0 0.00000
## State 3 0 0.0000000 0 0.00000
## State 4 0 0.0000000 0 0.00000Exploring Transition Probabilities and Intensities
It is also possible to look at the state transition matrix at different times and see how these probabilities change over time. Here we compute the transition matrix at 1 year.
pmatrix.msm(model_1, t = 1, covariates = "mean")## State 1 State 2 State 3 State 4
## State 1 0.8669 0.08101 0.008493 0.04357
## State 2 0.0000 0.75300 0.160340 0.08666
## State 3 0.0000 0.00000 0.716903 0.28310
## State 4 0.0000 0.00000 0.000000 1.00000and at 5 years.
pmatrix.msm(model_1, t = 5, covariates = "mean")## State 1 State 2 State 3 State 4
## State 1 0.4897 0.1761 0.07871 0.2556
## State 2 0.0000 0.2421 0.23419 0.5237
## State 3 0.0000 0.0000 0.18937 0.8106
## State 4 0.0000 0.0000 0.00000 1.0000Additionally, it is possible to examine the effect of covariates on transition probabilities. Here are the 5 year transition probabilities for a patient with a baseline age of 35.
pmatrix.msm(model_1, t = 5, covariates = list(years = 5, b_age = 35, dage = 20))## State 1 State 2 State 3 State 4
## State 1 0.5474 0.1674 0.07575 0.2095
## State 2 0.0000 0.2112 0.21622 0.5726
## State 3 0.0000 0.0000 0.16547 0.8345
## State 4 0.0000 0.0000 0.00000 1.0000and those who had the procedure at age 60.
pmatrix.msm(model_1, t = 5, covariates = list(years = 5, b_age = 60, dage = 20))## State 1 State 2 State 3 State 4
## State 1 0.3863 0.1409 0.06784 0.4050
## State 2 0.0000 0.2112 0.21622 0.5726
## State 3 0.0000 0.0000 0.16547 0.8345
## State 4 0.0000 0.0000 0.00000 1.0000Note that the transitions from CAV states are unaffected.
To summarize: Continuous Time Markov Chains provide a natural framework for working with multi-state survival models. The msm package is sufficiently sophisticated to permit modeling clinical process with level of fidelity that may provide insight about clinically observed disease progression. The software is relatively easy to use and there is plenty of documentation to help you get started.
Learning More About Multi-State Survival Models
To dive deeper into multi-state survival models, I am sure you will find Ardo van den Hout’ Multi-State Survival Models for Interval-Censored Data extraordinarily helpful. There are many good textbooks about the basics of Continuous Time Markov Chains. I recommend J.R.Norris’ - Markov Chains which is still modestly priced. There are also many expositions freely available on the internet including:
David F. Anderson - Chapter 6: Continuous Time Markov Chains from Lecture Notes on Stochastic Processes with Applications in Biology
Miranda Holmes-Cerfon - Lecture 4: Continuous-time Markov Chains
Søren Feodor Nielsen - Continuous-time homogeneous Markov chains
Karl Sigman - Continuous-Time Markov Chains
You may leave a comment below or discuss the post in the forum community.rstudio.com.